Merikanto

Trees & Graphs 不完全模板总结

Veröffentlicht am in
Symbole im Artikel gezählt: 1.2k Wörter Lesezeit ≈ 1 min

今天来总结一下树和图的解题套路。此篇包括：

  • 构造树
  • 树的遍历 （递归 & 迭代）
  • 网格遍历
  • 并查集 (Union Find)
  • 递归
  • 回溯 （治理分支污染）

树


构造树

1
2
3
4
5
6
TreeNode root = new TreeNode(value);

root.left  = recursion(left);
root.right = recursion(right);

return root;

树的遍历 （递归 & 迭代）

遍历所有节点， 打印输出 (Link)


总结：

  • **BFS 节省时间**， DFS 节省空间
  • 剪枝： 不符合条件的直接结束，以免 TLE
  • BFS 解决最短路，DFS 解决连通性

BFS

每层遍历。本质还是和 DFS-前序 很像，都是遵循 root - left - right 的顺序。


迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public void bfs(TreeNode root) {
    
    if (root == null) return root;
    
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    
    while (!q.isEmpty()) {
        for (int i = q.size(); i > 0; ++i) {
            TreeNode node = q.poll();
            System.out.print(node.val);		// 打印输出
            
            if (node.left != null)  q.offer(node.left);
            if (node.right != null) q.offer(node.right);
        }
    }
 	return;   
}

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public void bfs(TreeNode root) {
    
    int d = depth(root);
    
    for (int level = 0; level < d; ++level)
        printPath(root, level);	
}

// 递归打印，顺序： root - left - right
private void printPath(TreeNode root, int level) {		
    
    if (root == null) return root;
    if (level == 0) System.out.print(root.val);
    else {
        printPath(root.left,  level - 1);
        printPath(root.right, level - 1);
    } 
}

// 用 DFS-前序 找一共有几层 (maxDepth)
private int depth(TreeNode root) {			
    
    if (root == null) return 0;
    
    int l = depth(root.left);
    int r = depth(root.right);
    
    return Math.max(l, r) + 1;
}

DFS （前序）

顺序： root - left - right


递归

1
2
3
4
5
6
7
8
public void dfs(TreeNode root) {
    
    if (root == null) return root;
    
    System.out.print(root.val);		// DFS 的变形，条件判断写在这一行
    dfs(root.left);
    dfs(root.right);
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void dfs(TreeNode root) {
    
    if (root == null return root);
    
    Stack<TreeNode> s = new Stack<>();
    s.push(root);
 // Stack<Integer>  n = new Stack<>();
 // n.push(1);
    
    while (!s.isEmpty()) {
     // int tmp = n.pop();
        TreeNode node = s.pop();
        System.out.print(node.val);		// 打印输出

        // right 先压栈才是 preorder，因为栈是 LIFO
        if (node.right != null) s.push(node.right);		
        if (node.left != null)  s.push(node.left);
    }
    return;
}

后序

顺序： left - right - root


递归

1
2
3
4
5
6
7
8
public void postorder(TreeNode root) {
    
    if (root == null) return root;
    
    postorder(root.left);
    postorder(root.right);
    System.out.print(root.val);		// Postorder 的变形，条件判断写在这一行
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public void postorder(TreeNode root) {
    
    if (root == null) return root;
    
    // 需要用两个 stack，一个记录 node， 一个记录打印顺序
    Stack<TreeNode> path = new Stack<>();	
    Stack<TreeNode> s = new Stack<>();		
    s.push(root);
    
    while (!s.isEmpty()) {
        TreeNode node = s.pop();
        path.push(node);	// 这里。DFS前序是直接打印，后序是放进 path stack			
        
        // left 先压栈才是 postorder，因为这里用了两个栈
        if (node.left != null)  s.push(node.left);			
        if (node.right != null) s.push(node.right);		
    }
    
    // LIFO，左边最后进，最先出
    while (!path.isEmpty())  System.out.print(path.pop());			
    
    return;
}

中序

顺序： left - root - right


递归

1
2
3
4
5
6
7
8
public void inorder(TreeNode root) {
    
    if (root == null) return root;
    
    inorder(root.left);
    System.out.print(root.val);		// Inorder 的变形，条件判断写在这一行
    inorder(root.right);
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void inorder(TreeNode root) {
    
    if (root == null) return root;
    
    // 不用放 root，因为不是从 root 开始的
    Stack<TreeNode> s = new Stack<>();		
    
    while (!s.isEmpty() || root != null) {	// 注意条件
        
        if (root != null) {		// 注意判断
            s.push(root);
            root = root.left;
        }
        else {
            root = s.pop();		// 这里直接用 root，不需要用 TreeNode node
            System.out.print(root.val);		// 逻辑判断替换此行
            root = root.right;
        }
    }
 	return;   
}

图


网格遍历

网格类问题 DFS 通用思路

和二叉树的 DFS 类比。

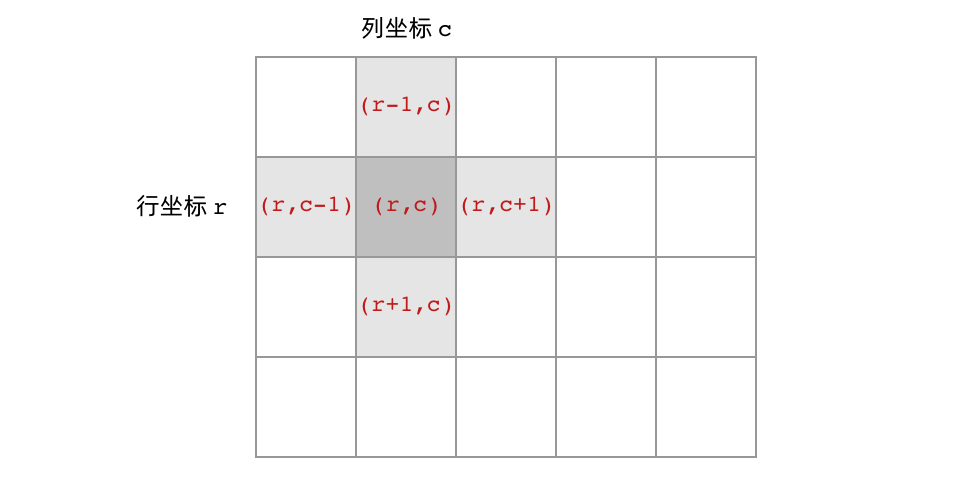
首先，网格结构中的格子有多少相邻结点？答案是上下左右四个。对于格子 (r, c) 来说（r 和 c 分别代表行坐标和列坐标），四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说，**网格结构是「四叉」的**。


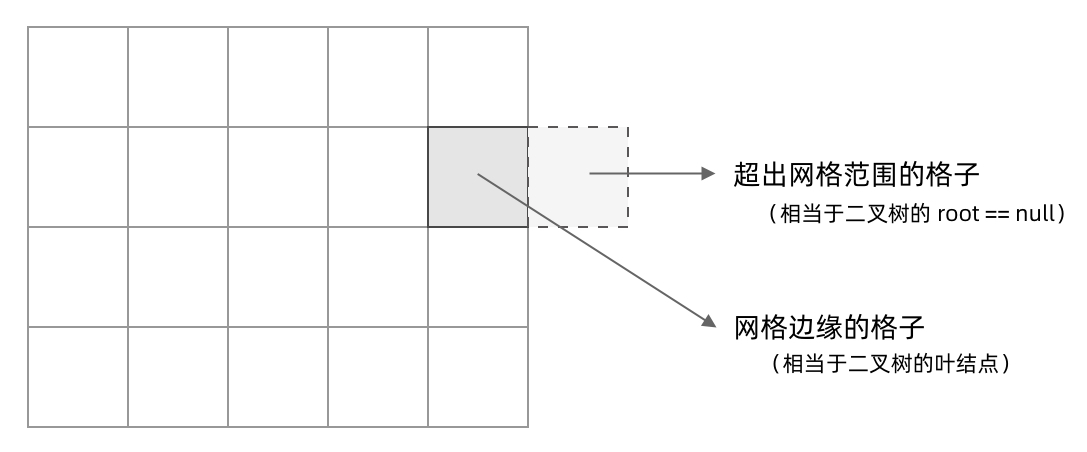
网格 DFS 中的 base case :

不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子，也就是那些超出网格范围的格子。


网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于，遍历中可能遇到遍历过的结点。 (因为图是连通的)

避免重复遍历: 标记已经遍历过的格子

每走过一个陆地格子，就把格子的值改为 2，这样当我们遇到 2 的时候，就知道这是遍历过的格子了。
也就是说，每个格子可能取三个值：

  • 0 —— 海洋格子
  • 1 —— 陆地格子（未遍历过）
  • 2 —— 陆地格子（已遍历过）

框架代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public void dfs(int[][] grid, int r, int c) {
    		
    // 判断 base case： 如果坐标 (r, c) 超出了网格范围，直接返回
    if (!inArea(grid, r, c))  return;	
    
    // 如果这个格子不是岛屿，直接返回
    if (grid[r][c] != 1)  return;		
    
    // 将格子标记为「已遍历过」
    grid[r][c] = 2; 			
    
    // 访问上、下、左、右四个相邻结点
    dfs(grid, r - 1, c);		
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

// 判断坐标 (r, c) 是否在网格中
public boolean inArea(int[][] grid, int r, int c) {
    return 0 <= r && r < grid.length;		// r 的左右区间
        && 0 <= c && c < grid[0].length;	// c 的左右区间
}

实战： Number of Islands (LC 200)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public int numIslands(char[][] grid) {
    
    int count = 0;
    for(int i = 0; i < grid.length; ++i) {		// i - r: row
        for(int j = 0; j < grid[0].length; j++) {	// j - c: column
            if(grid[i][j] == '1') {
                count++;
                dfs(grid, i, j);
            }
        }
    }
    return count;
}


private void dfs(char[][] grid, int i, int j) {
    
    if (i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] != '1') return;

    // 已经遍历过的，保存为 2
    grid[i][j] = 2; 		

    dfs(grid, i + 1, j);
    dfs(grid, i, j + 1);
    dfs(grid, i - 1, j);
    dfs(grid, i, j - 1);
}

并查集

LC Link

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class UnionFind {
    
    private Map<Integer,Integer> father;
    
    // 定义
    public UnionFind() {
        father = new HashMap<Integer,Integer>();
    }

    // 添加
    public void add(int x) {
        if (!father.containsKey(x))
            father.put(x, null);
    }

    // 合并
    public void merge(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);

        if (rootX != rootY)  father.put(rootX,rootY);
    }

    // 查找
    public int find(int x) {
        int root = x;

        while(father.get(root) != null)
            root = father.get(root);

        while(x != root){
            int original_father = father.get(x);
            father.put(x,root);
            x = original_father;
        }
        return root;
    }

    // 是否连通
    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }
}

实战： Gifting Groups / Friend Circle (LC 547)

题目分析：

  1. 考察连通分量的数目，所以我们要在模板中额外添加一个变量去跟踪集合的数量（有多少棵树）。
  2. 添加的时候把集合数量加一
  3. 合并的时候让集合数量减一

用并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class Solution {
    public int findCircleNum(int[][] isConnected) {
        
        // class instantiation
        UnionFind uf = new UnionFind();				
        
        for(int i = 0; i < isConnected.length; ++i){
            uf.add(i);
            
            for(int j = 0; j < i; ++j)
                if(isConnected[i][j] == 1)  uf.merge(i,j);
        }
        return uf.getNumOfSets();
    }
}


// 模版 (模版以外，新添加的内容，注释写在每行后面)
class UnionFind {
    
    private Map<Integer,Integer> father;	// 记录父节点
    
    //【新内容】（numOfSets 记录集合的数量）
    private int numOfSets;				
    
    // 定义 Constructor
    public UnionFind() {
        father = new HashMap<Integer,Integer>();
        
        // 【新内容】
        numOfSets = 0					
    }

    // 【新内容】
    public int getNumOfSets() {			
        return numOfSets;
    }
    
    // 添加
    public void add(int x) {
        if (!father.containsKey(x)) {
            father.put(x, null);
            
            // 【新内容】
            numOfSets++;				
        }
    }

    // 合并
    public void merge(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);

        if (rootX != rootY)  {
            father.put(rootX,rootY);
            
            // 【新内容】
            numOfSets--;				
        }
    }

    // 查找
    public int find(int x) {
        int root = x;

        while(father.get(root) != null)
            root = father.get(root);

        while(x != root){
            int original_father = father.get(x);
            father.put(x,root);
            x = original_father;
        }
        return root;
    }

    // 是否连通
    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }
}

递归 & 回溯


递归

两篇文章

Link 1

Link 2

简单总结：

分析问题我们需要采用自上而下的思维，而解决问题有时候采用自下而上的方式能让算法性能得到极大提升

e.g. Climbing Stairs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;

    int result = 0;
    int pre = 1;
    int next = 2;
    
    for (int i = 3; i < n + 1; i ++) {
        result = pre + next;
        pre = next;
        next = result;
    }
    return result;
}

改造后的时间复杂度是 O(n), 而由于我们在计算过程中只定义了两个变量（pre，next），所以空间复杂度是O(1)


回溯


治理分支污染

防止分支污染： ( e.g. 3 Sum )


  • 1 ) 每个分支都创建一个新的list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private void combSum(List<Integer> cur, int sums[], int target) {
     
    // 结束条件
     if (target == 0)  return;		

    // n叉树，length就是分支数量
     for (int i = 0; i < sums.length; i++) {	
         
        // 逻辑处理, 如果当前值大于target我们就不要选了
        if (target < sums[i]) continue;		
        
        // 由于List是引用传递，所以这里要重新创建一个，拷贝 cur
        List<Integer> list = new ArrayList<>(cur);   
        list.add(sums[i]);							 
        
        combSum(list, sums, target - sums[i]);	// 递归调用
    }
    return;
}

但每次都重新创建数据，运行效率很差。第二种方法：


  • 2) 回溯算法： 从分支1执行到分支2的时候，把分支1的数据给删除

    动画： Link

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private void combSum(List<Integer> cur, int sums[], int target) {
     
     if (target == 0)  return;			// 结束条件

     for (int i = 0; i < sums.length; i++) {

        if (target < sums[i]) continue;		
        
        // ** 路径添加，然后参与下一轮的递归
        cur.add(sums[i]);				
        combSum(list, sums, target - sums[i]);	
        
        // ** 路径回溯【最关键一步】  sum[i] 已经用完了
        // 为什么用完： 递归调用了结束条件，已经结束了； 或者开始下一轮分支选择
        cur.remove(cur.size() - 1);		
    }									
    return;								
}

回溯实质上是一种暴力算法，所以很多时候我们需要 剪枝操作

  • 去除不必要的分支，减少时间

关于N皇后：

https://cloud.tencent.com/developer/article/1424758